Beams - Fixed at One End and Supported at the Other - Continuous and Point Loads

• Beams - Supported at Both Ends - Continuous and Point Loads
• Beams - Fixed at One End and Supported at the Other - Continuous and Point Loads
• Beams - Fixed at Both Ends - Continuous and Point Loads

Beam Fixed at One End and Supported at the Other - Single Point Load

Bending Moment

M_A = - F a b (L + b) / (2 L²)                               (1a)

where

M_A = moment at the fixed end (Nm, lb_f ft)

F = load (N, lb_f)

M_F = R_b b                               (1b)

where

M_F = moment at point of load F (Nm, lb_f ft)

R_b = support load at support B (N, lb_f)

Deflection

δ_F = F a³ b² (3 L + b) / (12 L³ E I)                                  (1c)

where

δ_F = deflection (m, ft)

E = Modulus of Elasticity (Pa (N/m²), N/mm², psi)

I = Area Moment of Inertia (m⁴, mm⁴, in⁴)

Support Reactions

R_A = F b (3 L²- b²) / (2 L³)                                 (1d)

where

R_A = support force in A (N, lb_f)

R_B = F a² (b + 2 L) / (2 L³)                                 (1f)

where

R_B = support force in B  (N, lb_f)

Beam Fixed at One End and Supported at the Other - Continuous Load

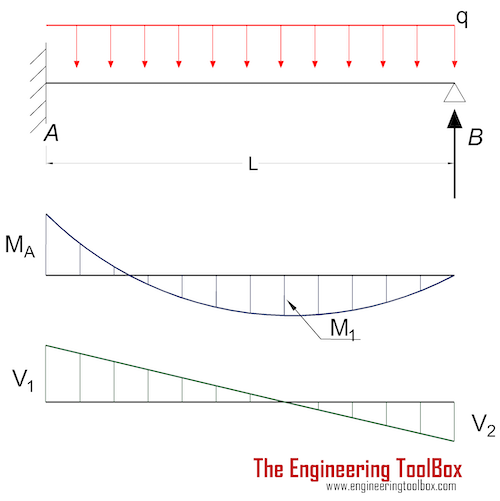Bending Moment

M_A = - q L² / 8                                    (2a)

where

M_A = moment at the fixed end (Nm, lb_f ft)

q = continuous load (N/m, lb_f/ft)

M₁ = 9 q L² / 128                                       (2b)

where

M₁ = maximum moment at x = 0.625 L  (Nm, lb_f ft)

Deflection

δ_max = q L⁴ / (185 E I)                                  (2c)

where

δ_max = max deflection at x = 0.579 L (m, ft)

δ_1/2 = q L⁴ / (192 E I)                                  (2d)

where

δ_1/2 = deflection at x = L / 2   (m, ft)

Support Reactions

R_A = 5 q L / 8                            (2e)

R_B = 3 q L / 8                            (2f)

Beam Fixed at One End and Supported at the Other - Continuous Declining Load

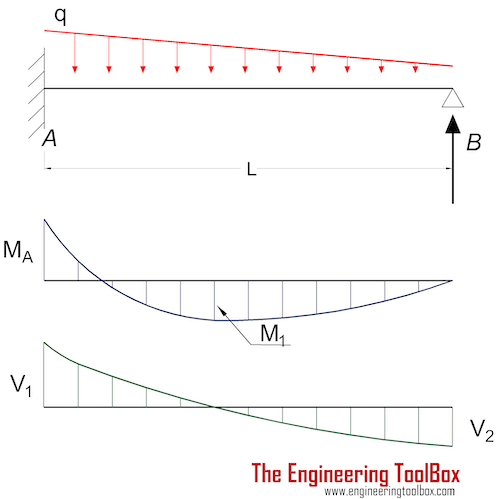Bending Moment

M_A = - q L² / 15                               (3a)

where

M_A = moment at the fixed end (Nm, lb_f ft)

q = continuous declining load (N/m, lb_f/ft)

M₁ = q L² / 33.6                              (3b)

where

M₁ = maximum moment at x = 0.553 L (Nm, lb_f ft)

Deflection

δ_max = q L⁴ / (419 E I)                                  (3c)

where

δ_max = max deflection at x = 0.553 L   (m, ft)

δ_1/2 = q L⁴ / (427 E I)                                  (3d)

where

δ_1/2 = deflection at x = L / 2   (m, ft)

Support Reactions

R_A = 2 q L / 5                            (3e)

R_B = q L / 10                            (3f)

Beam Fixed at One End and Supported at the Other - Moment at Supported End

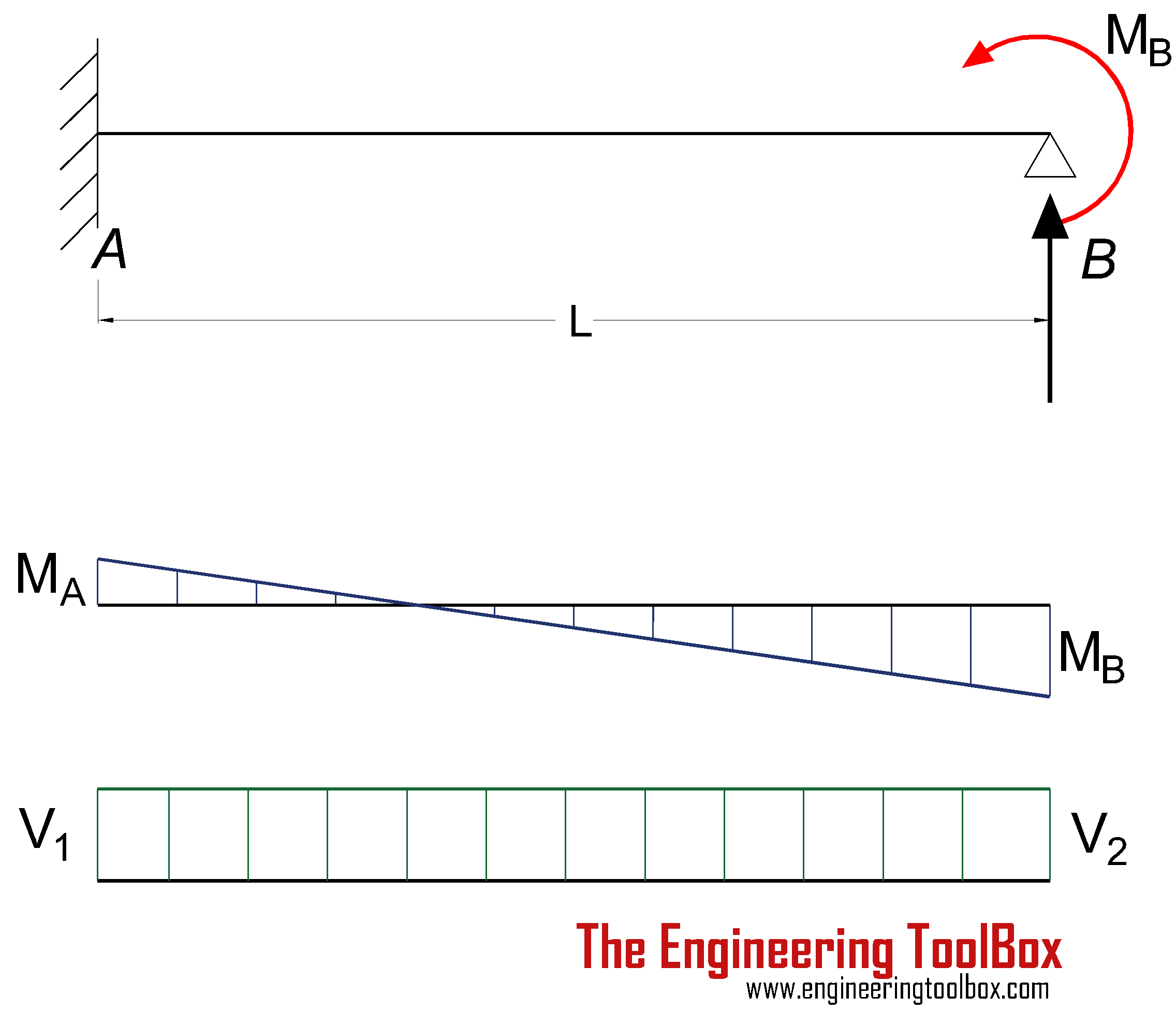Bending Moment

M_A = -M_B / 2                               (4a)

where

M_A = moment at the fixed end (Nm, lb_f ft)

Deflection

δ_max = M_B L² / (27 E I)                                  (4b)

where

δ_max = max deflection at x = 2/3 L   (m, ft)

Support Reactions

R_A = 3 M_B / (2 L)                                 (4c)

R_B = - 3 M_B / (2 L)                                (4d)