Beams Natural Vibration Frequency

Vibrations in a long floor span and a lightweight construction may be an issue if the strength and stability of the structure and human sensitivity is compromised. Vibrations in structures are activated by dynamic periodic forces - like wind, people, traffic and rotating machinery.

There are in general no problems with vibrations for normal floors with span/dept ratio less than 25. For lightweight structures with span above 8 m (24 ft) vibrations may occur. In general - as a rule of thumb - the natural frequency of a structure should be greater than 4.5 Hz (1/s) .

Structures with Concentrated Mass

f = (1 / (2 π)) (g / δ)^0.5                                     (1)

where

f = natural frequency (Hz)

g = acceleration of gravity (9.81 m/s²)

δ = static dead load deflection estimated by elastic theory (m)

Note! - static dead load for a structure is load due to it's own weight or the weight of mass that is fixed to the structure.

Structures with Distributed Mass

General rule for most structures

f = a / (δ)^0.5                                    (2)

a = numerical factor (in general 18)

The numerical factor a can be calculated to 15.75 for a single lumped system but varies in general between 16 and 20 for similar systems. For practical solutions a factor of 18 is considered to give sufficient accuracy.

Simply Supported Structure - Mass Concentrated in the Center

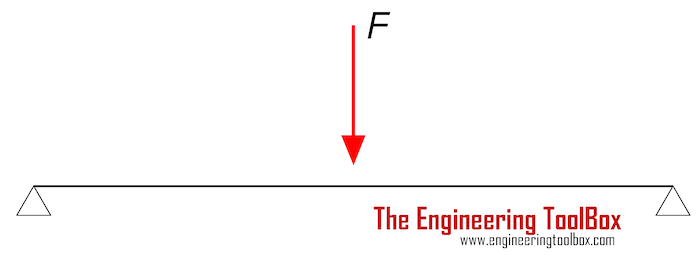
For a simply supported structure with the mass - or load due to gravitational force weight - acting in the center, the natural frequency can be estimated as

f = (1 / (2 π)) (48 E I / M L³)^0.5                                    (3)

where

M = concentrated mass (kg)

Simply Supported Structure - Sagging with Distributed Mass

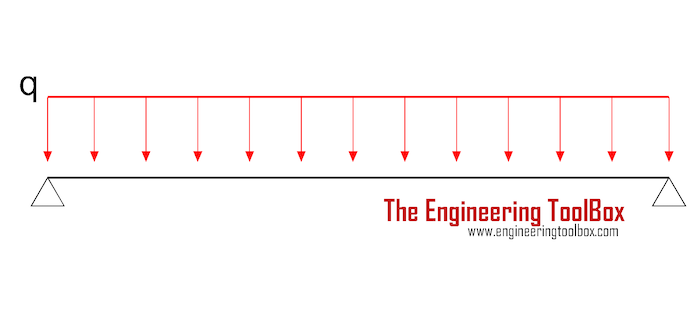
For a simply sagging supported structure with distributed mass - or load due to gravitational force - can be estimated as

f = (π / 2) (E I / q L⁴)^0.5                                 (4)

Example - Natural Frequency of Beam

The natural frequency of an unloaded (only its own weight - dead load) 12 m long DIN 1025 I 200 steel beam with Moment of Inertia 2140 cm⁴ (2140×10^-8 m⁴) and Modulus of Elasticity 200×10⁹ N/m² and mass 26.2 kg/m can be calculated as

f = (π / 2) ((200×10⁹ N/m²) (2140×10^-8 m⁴) / (26.2 kg/m) (12 m)⁴)^0.5

= 4.4 Hz  - vibrations are likely to occur

The natural frequency of the same beam shortened to 10 m can be calculated as

f = (π / 2) ((200×10⁹ N/m²) (2140×10^-8 m⁴) / (26.2 kg/m) (10 m)⁴)^0.5

= 6.3 Hz  - vibrations are not likely to occur

Simply Supported Structure - Contraflexure with Distributed Mass

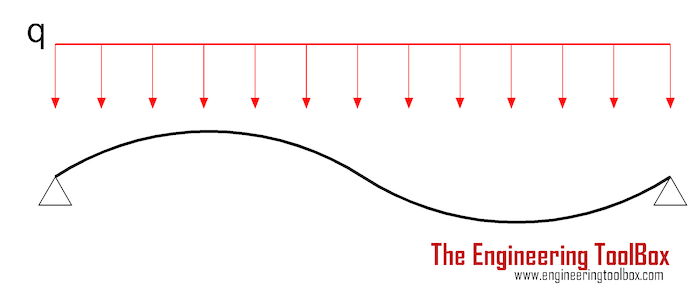
For a simply contraflexure supported structure with distributed mass - or dead load due to gravitational force - can be estimated as

f = 2 π (E I / q L⁴)^0.5                                      (5)

Cantilever with Mass Concentrated at the End

For a cantilever structure with the mass - or dead load due to gravitational force - concentrated at the end, the natural frequency can be estimated as

f = (1 / (2 π)) (3 E I / F L³)^0.5                              (6)

Cantilever with Distributed Mass

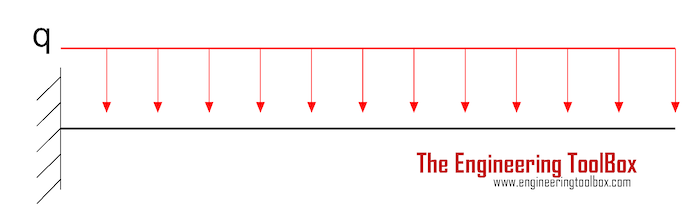
For a cantilever structure with distributed mass - or dead load due to gravitational force - the natural frequency can be estimated as

f = 0.56 (E I / q L⁴)^0.5                                    (7)

Structure with Fixed Ends and Distributed Mass

For a structure with fixed ends and distributed mass - or dead load due to gravitational force - the natural frequency can be estimated as

f = 3.56 (E I / q L⁴)^0.5                          (8)